LeetCode题解：Path In Zigzag Labelled Binary Tree

本文为LeetCode 1104. Path In Zigzag Labelled Binary Tree 的题解。

题目描述

一棵无穷的二叉树，每个节点都编号（label）了：对于奇数层（第1、3、5等层），从左向右编号。对于偶数层，从右向左编号。但是每层的编号还是最小2^(level-1),最大2^level-1。

如图：

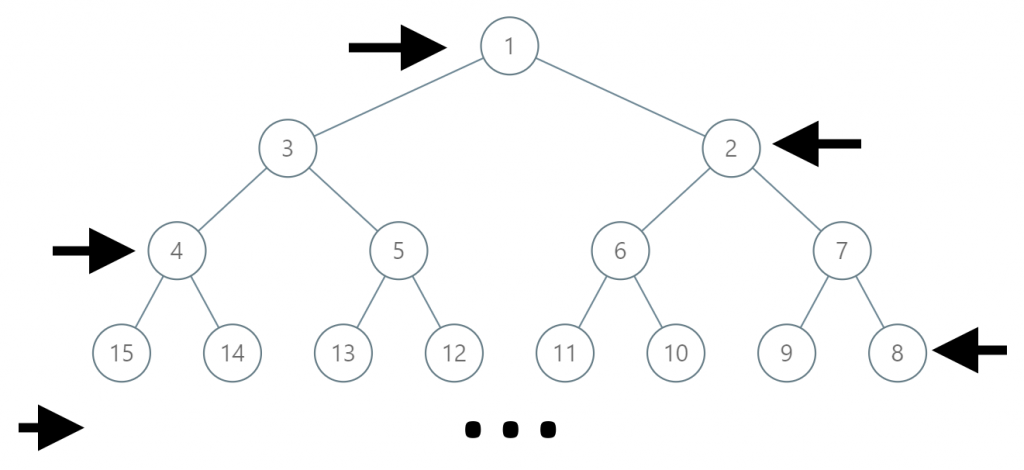
给你一个编号（label），输出从顶层到该节点经过的节点编号。

Example 1:

Input: label = 14
Output: [1,3,4,14]

Example 2:

Input: label = 26
Output: [1,2,6,10,26]

思路

1. 给定节点，我们可以知道节点在第几层
2. 给定正常树中的编码，可以知道父节点的编号。
3. 给定正常树中的编码，可以知道在该变异树中的节点编号。

第一点是显而易见的，log(label)即为层数。

第二点，正常节点的值label除以2即为父节点的label。

对于第三点，在level层，变异树中的节点label和正常树的节点label（也就是树中堆成位置的节点）之和为2^(level-1)*3-1。

比如图中第四层，14节点在正常编码的时候是9，14+9=2^(4-1)*3-1=23。

这样，我们只需要在正常树中向上回溯到根节点就好，只是在放结果的时候，转化为变异树的label值即可。

代码

import java.util.Arrays;
import java.util.List;

/**
 * https://www.robberphex.com/path-in-zigzag-labelled-binary-tree/
 */
class Solution {
    /**
     * 计算label节点在第几层
     */
    private int level(int label) {
        int level = 0;
        while (label != 0) {
            level += 1;
            label >>= 1;
        }
        return level;
    }

    /**
     * 计算第level层的label节点变换后的位置
     * <p>
     * 如果输入变异节点，则输出正常节点
     * 反之亦然
     */
    private int normalLabel(int label, int level) {
        if (level % 2 == 0) {
            int base = 1 << (level - 1);
            int sum = base * 3 - 1;
            label = sum - label;
        }
        return label;
    }

    public List<Integer> pathInZigZagTree(int label) {
        int totelLevel = level(label);
        Integer[] res = new Integer[totelLevel];

        // 我们需要在正常树中回溯
        // 故先将输入节点替换为正常树中的节点
        label = normalLabel(label, totelLevel);

        // 树的回溯
        while (label != 0) {
            int level = level(label);
            res[level - 1] = normalLabel(label, level);
            label /= 2;
        }
        return Arrays.asList(res);
    }

    public static void main(String[] args) {
        List<Integer> res = new Solution().pathInZigZagTree(33);
        System.out.println(res);
        // 输出 [1, 2, 7, 8, 31, 33]
    }
}